P10612 Box of Mirrors 题解

我发现我贪心之类的什么都不会，因此我们用一点点置换群知识暴力构造！

由于光路可逆，因此我们只保留一边的光线和对应的出口。我们保留左边和下边的光线。我们经过观察发现，镜子只会使光向右和向上走，并且每个光线恰好对应一个出口。

我们可以用一个 的置换来描述光线和终点的关系，记作 ， 表示标号 的光线最后的出口相对的编号，这样就是一个 的置换。

继续观察，考虑放置镜子的实质。实际上就是交换进入格子的两束光的终点。但是有一个问题，直接放置可能会改变之后可以进行的操作。

考虑样例里的这张图：

样例图片

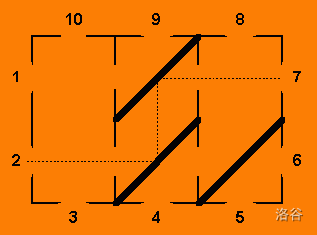
如果你先放置最后一行第二个镜子，那么放置第一行第二个镜子的效果就变成了交换光线 的终点。我们接下来用 来表示这个对换。

注意到光线只会往右上方走，因此只会对右上方的镜子效果造成影响。我们从右上角往左下放置镜子即可。

我们从第一行开始，从上到下，每行从右往左放置镜子。我们发现每行实现的对换形如 其中对于 ，有 。这是一个轮换。

因此，我们考虑的就是通过若干的轮换的复合能否构成 。

考虑对这个置换进行轮换分解。假设目前是第 行，所在的轮换是 ，其中 是行的编号， 是列的编号。

首先我们把 拆出来。因为只有这一行可以进行和 相关的轮换。变成：

此时我们有两种选择，一种之把 也拆出来，需要保证下一个数不是 ：

另外一种则是把 转到前面来，然后拆出来。

此时我们可以把 先转到开始然后继续从后面拿。只要最后的数小于 ，就可以继续。但是取完后面的数一次之后就只能从后面开始取了。

考虑如何决定选择哪种操作。贪心地想应该选择两个数中比较大的那个。

• 如果比较大的是 ，那么显然多拿没坏处。如果接下来的数比自己小不影响，比自己大的话就可以创造更多连续取数的机会。
• 如果比较大的是 ，那么 的前一个数比 大，那么拿走不影响。否则也可以创造更多连续取数字的机会。

但这只是感性理解。我们考虑严格证明。

首先考虑若干个形如 的轮换复合长什么样子。从 个轮换开始。我们只保留其中的重复元素，不重复的元素用省略号代替（注意整个 仍然保证单调递减）。

先都拆出来一个 出来。

把中间两个轮换都转一下，然后拆出来 化简：

中间两个轮换已经没有相交部分了，我们交换之后和两边的轮换合并起来。注意中间两个轮换省略号省略的内容就是在 和 并且递减的序列，因此两个轮换后面的部分仍然递减：

我们发现，如果两个轮换有相交，我们可以挑出两个相交的元素并使得这两个元素最终只在其中一个轮换中存在。这样化简之后的最坏情况就是相邻两个轮换只有一个元素相交。此时我们考虑把这些轮换拼起来：

注意到前后两个省略号一个是前面一部分小于 的数，另一部分是大于 的，因此我们可以直接合并起来。

我们再加入一个数试试：

我们发现，最后的结果一定是 和一段下降的 交替出现。

如果不相交的话，相当与被轮换分解时拆成了两个轮换了。

接下来我们证明，此类轮换一定可以通过上述方法分解出来。我们使用归纳法。

首先考虑轮换内部只包含 个 的情况。显然就直接拆完了。

考虑有 个 的情况。

注意到我们的贪心策略的停止条件实际上就是最后的数大于前面的数。因此我们把前面的数转到后面之后仍然能保证单调递减。此时变成了大小为 的子问题，根据归纳法可知原命题成立。

代码和勘误稍后放在这里。